TORQUE Name:___________________________Date/Time:___________

Purpose: To investigate torque by doing the following activities:
    a. Measuring an unknown mass
    b. Measuring the mass of a meter stick
    c. Calculating clockwise and counter clockwise torques

Apparatus: Meter stick, knife edge clamp, knife edge support, mass hangers(3), mass set, lab jack, electronic balance, and string loops.

Theory: Introduction to torque

Think about the everyday activity of opening a door, just for a moment.

Q: What do you think you do to the door, when you open it?

A: You apply a torque.

Torque = Lever-arm X Force; Torque is a vector. Torque comes in clockwise and counter clockwise directions. Clockwise direction is the direction in which a mechanical clock turns. The opposite direction is called counter clockwise.

The door knob is kept away from the hinge in order to have a greater lever-arm. Imagine how hard it will be to open, if the knob is kept closer to the hinge.

Lever-Arm is the perpendicular distance to the force.

a. Measuring an unknown mass

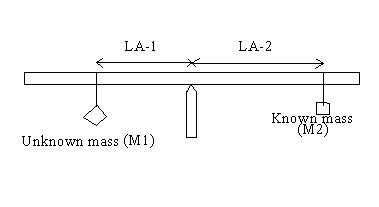
Meter stick is supported at the center of gravity.

Unknown mass will try to rotate the meter stick counter clockwise and known mass will try to rotate the meter stick clockwise.

Counter clockwise torque = Unknown mass X Lever-Arm-1

Clockwise torque = Known mass X Lever-Arm-2

For balance, counter clockwise torque must equals the clockwise torque.

Unknown mass X Lever-Arm-1 = Known mass X Lever-Arm-2

Unknown mass = [Known mass X Lever-Arm-2] ÷ [Lever-Arm-1]

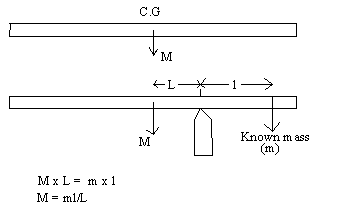
b. Measuring the mass of a meter stick (M)

Now you need to move the support point away from the center of gravity (C.G). This way you get the rotation effect of M, mass of the meter stick.

Use the following formula to calculate the % Difference:

%Difference = (Difference/Average)x100, where Difference is the difference between the two measured values, and Average is the average of the two measured values.

Procedure and Data:

a) To find the unknown mass

1. Find the center of gravity of the meter stick by balancing it on the support stand. Use a knife-edge clamp on the meter stick. Record the results to the nearest tenth of a centimeter.

2. Hang the unknown mass near one end of the stick. Hang a 200-g mass near the other end of the stick and obtain the balance. Record the locations of the masses.

3. Calculate the value of the unknown mass.

4. Repeat 2 & 3 for known masses 250-g and 300-g and complete the data table.

a. Unknown mass, M1

Meter stick is supported at the C.G.

Location of the center of gravity (C.G) = ________ cm

Location of the unknown mass = _________ cm _________cm ___________cm

Location of the known mass = _________ cm _________cm ___________cm

M1 x LA-1 = M2 x LA-2; M1 = (M2 x LA-2)/LA-1

Known mass, M2(g)	Lever-arm for known mass, LA-2	Lever-arm for unknown mass, LA-1	Unknown mass, M1
200	-	-	-
250	-	-	-
300	-	-	-
Average of the unknown mass, M1			-
Unknown mass measured using electronic balance			-
% difference			-

b. Mass of a meter stick, M:

1. Hang a 100-g mass near one end of the stick. Slide the stick through the supporting clamp and obtain the balance. Record the location of the support point and the location of the 100-g mass.

2. Calculate M.

3. Repeat 1 & 2 with 150-g and 200-g known masses and complete the data table.

Meter stick is supported at a point away from the C.G.

Location of the center of gravity (C.G) = ________ cm.

Location of the support point = ________ cm __________cm ___________cm

Location of the known mass = ________ cm __________cm ___________cm

Known mass, m (g)	Lever-arm for known mass, l	Lever-arm for mass of meter stick, L	Mass of meter stick, M
100	-	-	-
150	-	-	-
200	-	-	-
Average of the mass of meter stick, M			-
Mass of meter stick measured using electronic balance			-
% difference			-

c) Torques

1. With the meter stick on the support stand at X₀ (center of gravity) suspend a 150-g mass at the 10 cm mark and a 200-g mass at 90 cm mark. Hang a 100-g and adjust its position to obtain static equilibrium.

2. Record the location of the 100-g mass, and determine the experimental value of the lever-arm for the 100-g mass.

3. Draw a free-body diagram of the meter stick and show all the forces acting on it.

4. Write an equation by balancing the torques.

5. Calculate the lever-arm for the 100-g mass, using the above equation, and compare it with the experimental value.

6. Use the experimental value of the lever-arm for the 100-g mass to calculate the counterclockwise and clockwise torques about X₀ and complete the data table below:

DATA:

Location of the 100-g mass = ___________

Experimental value of the lever-arm for the 100-g mass = ___________

Calculated value of the lever-arm for the 100-g mass = ___________

% Difference = ___________

Counterclockwise torque about X₀ = _________

Clockwise torque about X₀ = ____________

% difference = _________

Problem 1: A meter stick has a mass of 140-g and center of mass at 49.5 cm. This meter stick is supported at the center of mass. An unknown mass is hanged at 19.5 cm. Balance is obtained when 150-g is hanged at 69.5 cm. Draw a free body diagram for the meter stick and determine the unknown mass.

Problem 2: A uniform meter stick is supported at the 40.0 cm mark. Balance is obtained when a 45.0 gram mass is suspended at the 10.0 cm mark. Draw a free body diagram for the meter stick and determine the mass of the meter stick.